返回

第九章 日食原理

一、月影轴、本影、伪本影、半影、日食类型

月亮遮住了太阳光，使地球在的人们看不见太阳或只看到太阳的一部分，便形成了日食。在任意时刻，月亮的影子总在存在的，当地球进入月亮影子区域，才能看到日食现象。

当角度满足一定条件时才能发生日食。即月亮应在地球和太阳之间才可能发生日食。即日月合朔时刻（或此刻附近）才可能发生日食。如果日月合朔时，月亮位置太“高”或太“低”，影子落在地球的上方（北极之上）或下方（南极之下），地球上看不到日食。

当距离满足一定条件时才能发生全食。设地球的赤道半径为1，那么月亮的影子长度约为58.57。地球带着月球围绕着遥远的太阳公转，公转的轨道是个椭圆，所以月亮月有时离太阳近此，有时候远一些，所以影子长度约为58.57±1.67%，这个值与地月距离60.34很接近。月球绕地运动轨道是个偏心率较大的椭圆，地月距60.34±5.5%，因此地月距离可能小于影子长度，形成日食。

二、日食的周期性

三、空间直线与地球的交点

地球的形状可近似为旋转椭球，月影轴或月影锥的母线可以使用一条直线来描述。某时刻月影轴与地球的交点就是该时刻日食的中心点。影锥的各条母线与地球的交点构成影子在地球上的轮廓线。

利用直线的参数方程求解比较容易

以下示例程序计算直线与地球的交点，直线经过(x1,y1,z1)和(x2,y2,z2)两点，e为极赤径比，r为赤半径：
function lineEll(x1,y1,z1, x2,y2,z2, e,r){ //求空间两点连线与地球的交点(靠近点x1的交点)
  var dx=x2-x1, dy=y2-y1, dz=z2-z1, e2=e*e, A,B,C,D,R,t, p=new Object();
  A = dx*dx + dy*dy + dz*dz/e2;
  B = x1*dx + y1*dy + z1*dz/e2;
  C = x1*x1 + y1*y1 + z1*z1/e2 - r*r;
  p.D = B*B-A*C; if(p.D<0) return p; //判别式小于0无解
  D = sqrt(p.D); if(B<0) D = -D; //只求靠近x1的交点
  t = (-B+D)/A;
  p.x=x1+dx*t, p.y=y1+dy*t, p.z=z1+dz*t;
  R = sqrt(dx*dx + dy*dy + dz*dz);
  p.R1 = R*abs(t), p.R2 = R*abs(t-1); //单位是千米
  return p;
}

交点坐标(x,y,z)求出后，交点的经度α = atan2(y,x)，地理经度 L = α - g，地心纬度φ'为tanφ' = z / sqrt(x*x+y*y)。地心纬度φ'与地理纬度φ的关系为：tanφ' = (b/a)²tanφ，式中b/a是极半径比赤道半径。显然地心纬度小于地理纬度，在南北极和赤道上二者相等。

最后，地理经度应限制在-180°到+180°,地理纬度应限制在-90°到90°。西方著作中，地理经度往往是向西为正，那么有L = g - α

四、日食计算所用的坐标系

并没有硬性规定要用哪种类型的坐标系。一般的说，精确的日食计算中，常常用到直角坐标系。

（一）坐标变换
　球面转直角坐标llr2xyz()：
function llr2xyz(JW){
  var r=new Array(),J=JW[0],W=JW[1],R=JW[2];
  r[0]=R*cos(W)*cos(J);
  r[1]=R*cos(W)*sin(J);
  r[2]=R*sin(W);
  return r;
}
　直角转球面坐标xyz2llr()
function xyz2llr(xyz){
  var r=new Array(), x=xyz[0],y=xyz[1],z=xyz[2];
  r[2] = sqrt(x*x+y*y+z*z);
  r[1] = asin(z/r[2]);
  r[0] = rad2mrad( atan2(y,x) );
  return r;
}
　球面坐标旋转函数llrConv()：
function llrConv(A,E){
  var B=new Array(),J=A[0],W=A[1];
  B[0]=rad2mrad( atan2(sin(J)*cos(E) - tan(W)*sin(E), cos(J)) );
  B[1]=asin ( cos(E)*sin(W) + sin(E)*cos(W)*sin(J) );
  B[2]=A[2];
  return B;
}
　说明：转换函数中调用rad2mrad()函数的作用是将角度转换到0到2PI
　用法：B = llrConv(A,E)
　功能：由A道坐标转到B道坐标，E为A道与B道的夹角。
　A与B的起算点为A与B的交点，交点有升交点和降交点之分，起算点由用户任选，但应注意：在A道上沿经度测量方向走，经过起算点时，如果纬度增加，则表示起算点为升交点，这时E取正，反之为降点E取负。
　例1：A为黄道坐标，转换后B为赤道坐标，如果经度起算点为春风点，那么沿A道(即黄道)，经过春风点时，黄纬是增加的，所以E取正，E是黄赤交角。
　例2：A为赤道坐标，转换后B为黄道坐标，如果经度起算点为春风点，那么沿A道(即赤道)，经过春风点时，赤纬是增加的，所以E取负，E是黄赤交角。

（二）贝塞尔坐标系及其变换

贝塞尔坐标系的定义：

z轴经过地心且平行于月影轴，往太阳那个方向为正。垂直于月影轴且经过地心的平面为基面。基面与赤道面的交线为x轴，xyz三轴构成右手坐标系。如果规定x轴正方向的赤经比z轴赤经多90度而不是-90度，这样y轴总是在北半球。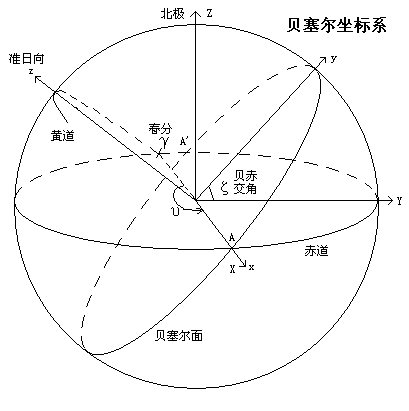

设z轴上某一点记坐B向量，写为直角坐标形式记作B[0,1,2]，jd时刻太阳赤道坐标为S[0,1,2]，月亮赤道坐标为M[0,1,2]，存在关系式B = S - M。应注意，这个关系式是一个矢量运算关系。当S、M为球面坐标时，请先将它们转为直角坐标，然后再运算。最后得到的B还可以转为球面坐标。因此，在球面坐标系中，z轴向量的赤道坐标表示：B = xyz2llr( llr2xyz(S) - llr2xyz(M) )。实际上，B的方向十分接近太阳，有中心线日食发生期间，B与S的角度差不到10角秒。

贝塞尔坐标变换三要素：

有了以下三个参数，就可以在贝塞尔坐标、赤道坐标、地理坐标之间进行坐标变换。
1、贝赤交角ζ
2、升交点赤经(A点的赤经,起算点赤经)υ
3、格林尼治恒星时GST（本文简写为g）

当z轴向量B求出后，贝赤交角立即得到：ζ= 90-B[1]，同时得到A点的赤经(起算点赤经)：υ = 90+B[0]。如果天体赤经要转换为以格林尼治子午圈起算的经度，则应将天体赤经减去格林尼治恒星时。格林尼治恒星时是一个角度量，它指格林尼治子午圈相对春风点的赤经(角度)。

已知天体赤道坐标P[]求其贝塞尔坐标：
　(1)先把P经度转为A点起算的经度P[0] = P[0]-υ
　(2)然后旋转P = llrConv(P,-ζ)。
　(3)因为在赤道上沿经度测量方向走，经过起算点A为降交点，所以这里ζ取负。通常，天体的贝塞尔坐标以直角坐标形式表达，所以还应计算P = llr2xyz(P)。
　例：已知月亮赤道坐标，求它的贝塞尔坐标。按以上三步骤即可。

已知天体贝塞尔坐标P[]求基赤道坐标：
　(1)P = xyz2llr(P)。
　(2)P = llrConv(P,ζ)
　(3)P[0] = P[0]+υ

用直角坐标进行贝、赤坐标变换

xyz是贝塞尔直角坐标系，XYZ是A点（贝赤交线上）起算的赤道直角坐标系。x轴与X轴重合，y轴向量(0,P,Q),z轴向量(0,-Q,P)，其中P = cosζ，Q = sinζ

地理坐标与贝塞尔坐标的转换：

我们在一个实际问题中求解。贝塞尔坐标中的点P(x,y,z)落在地球表面，z轴赤经赤纬是(υ,90-ζ)，格林尼治恒星时为g，地球赤道半径为a与极半径为b，若z未知，试求z的值。

五、贝塞尔坐标的其它问题

1、求贝圆的短半径：

从贝塞尔基面的定义知，贝塞尔基面与椭球形地球的交线为椭圆，下文称贝圆。贝圆的长半径在x轴，长度为地球赤道半径a。短半径在y轴，如何求其大小呢？我们引入下图，这是地球的一个剖面图，贝塞尔坐标的y轴落在剖面上，OD正是贝圆的半短径b₂，今设赤道半径为a，南北极半径为b。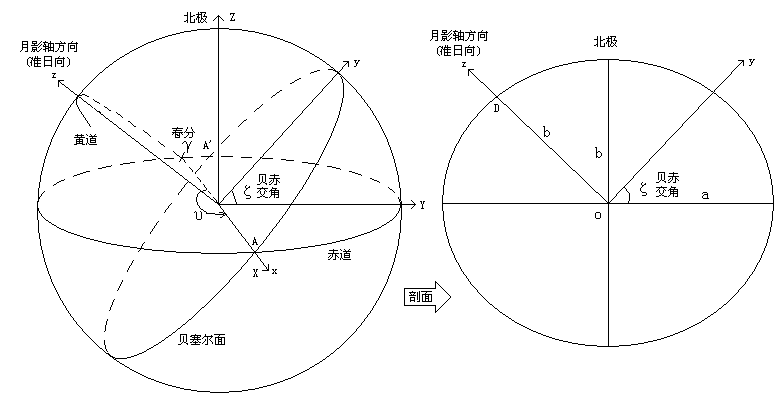

依上图建立椭圆方程 (x/a)²+(y/b)²=1，把x = -r*cosζ，y = r*sinζ代入得：
　b₂ = r = b/sqrt(1-c*cos²ζ)，式中c = 1-b²/a²=0.00669438
　ζ约等于“90-太阳赤纬”，即cosζ≈sinδ≈sinε*sinλ(其中ε为黄赤交角，λ为太阳黄经，δ为太阳赤纬)，且c*cos²ζ是个小量，因此上式可改写为：
　b₂ = b*(1+c*sin²δ/2) = b(1+0.0005296sin²λ)，其中地球偏率f=1/298.25642，b = 1-f，ε=84381.448角秒
　当影轴刚好扫过地球边缘，为了判断有无中心线，b₂通常它的最大可能值0.9972即可，不必取均值，其实南极大陆平均海拨也有2千米左右。

2、贝赤交线与贝黄交线的夹角

应用三垂线定理易证得自转轴总是在yz平面。由于太阳距我们很远，月球则要近得多，所以月球的移动对月影轴方向的影响是轻微的，月影轴的方向主要有太阳决定，基本与太阳相同，因此，如果太阳赤纬为负时，上图中y应画在北极左边。这就是说随着太阳运转，赤纬变化，北极在y轴上左右移动。

由于太阳黄纬小于2角秒且太阳视差小于10角秒，所以基面基本垂直于黄道面，当月影轴经过地球，基面与黄轴的夹角不超过10角秒。虽然，实际计算不推荐看成垂直，但建立这样一种概念有利于坐标变换。贝黄交角：约为90度。

下图则给出贝塞尔坐标、黄道、赤道、基面等的示意图：

图中∠BOA可按以下方法得到：由黄赤变换公式sinδ = sinβ cosε + cosβ sinε sinλ，A点赤纬是δ=0，B点黄经λ=υ，代入得tanβ = -tanε sinλ = -tanε sin(υ)。贝圆几乎垂直于黄道，所以A的黄纬β近似为∠BOA，则有tan∠BOA = -tanε sinυ

3、半影与贝圆的交点(求两圆交点,贝圆用地球平均半径)

4、半影与贝圆的交点(求两圆交点,贝圆看作椭圆)

方法与求角圆与圆的交点基本相同，但要多做一次重复计算。

5、半影与贝圆的交点(精确求法)

6、半影与贝圆的切点计算

六、在贝塞尔坐标系中求解地球表面某点的速度：

求某一地标(含海拔)的贝塞尔坐标

求影轴上某点对应的本影和半影半径

影子中心相对于观测点的速度

求某时刻的中心点

地心到直线的距离

距离改正

在贝塞尔坐标中，用两点法插值求地月距离(线性插值)，会产生一定的误差，建议进行二次函数修正。如图，影足由O运动到A用时T日，角速度为ω

R取地月平均值，以地球赤道半径为单位，即R=385000/6378=60.36，ω为日月黄经差的平均速度0.2128/日，则有f = 1.366(T²-t²)，t是以中点O起算的。如果t从B点起算，B运动开A用时T，则f = 1.366t(T-t)

日出日没食甚线的绘图方法

计算的点数是有限的，所以画出的日出日没食甚线不会刚好经过南北界线的头尾端点，以下算法解决上问题。

红线是半影直径，它垂直于影子的相对速度方向（影子相对交点上的观测者的速度，它与地球自转有关）。影子速度比贝塞尔平面上地球自转速度大许多，所以红线实际基本垂直于影速方向，倾斜不多。随着影子的移动，红线与贝圆的连续的交点构成日出没食甚线。

上图中的连接图：当北界不存在时，q1连续写点造成q3不存在，因此连线前构造一个q3，即在q3线头写入q1的最后一点；当北界存在时，q1线尾与q3线头分别补上北界的线头和线尾，产生的效果有两个，其一确保q1和q3不为空线，其二使线头连接到北界的端点。q2与q4处理的方法相同。

绘图方法：只要北界存在，不论q1和q3是否存在，q1线尾强制接北界头，q3线头强制接北界尾；如果不存在，q3必不存在，则强制补一个与q1连续的坐标生成一个q3。南界的处理方法类推。最后q1、q2线头连接，q3、q4线尾连接。
  1、q1、q2、q3、q4分别存储四条食甚线，q1、q3为食甚北线，q2、q4为食甚南线。北线写指针A指向q1或q3，南线写指针B指向q2或q4，初始状态A=q1，B=q2
  2、写点过程中，当时间已越过最大食时刻， 如果q1不存在则A移到q3，如果q2不存在则B移到q4。
  3、写点过程中，如有北线有断线（无解），则把A移到q3；如果南线断线，则B移到q4。
  4、四线段q1、q2、q3、q4全部写完之后：(1)如果无北界线q3必为空，在q3增补一个q1的末坐标，使q1和q3两线连续；如果有日食北界q1和q3均可能为空，q1末坐标加一个北界头坐标，q3首坐标加一个北界尾坐标。这样q1和q3构成完整的北食甚线。(2)q2、q4做同样处理，使用q2和q4变成完整的南食甚线
  5、南、北食甚线的线头和线尾分别，即q1和q2线头连接，q3和q4线尾连接。