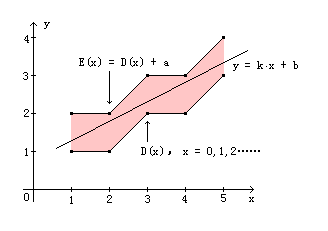|
第六章:离散序列的直线拟合算法 许剑伟 2008-12-2 于莆田十中 问题提出:已知古代朔日表,如何找到一条直线 y(x) = k·x + b 拟合朔日表,然后用[y(x)]表示朔日,x表示朔日序数(x=0,1,2……),k和b是待求系数。 数学模型:设某一组实测的离散数据序列D(x),其中x = 0,1,2……。现求解一条直线 y(x) = k·x + b,使y(x)在 x = 0,1,2……的值与实测值的误差大等于0小于a。对于上述问题,a取值为1,遗憾的是这个问题不能使用最小二乘法直接求解,我们考虑其它方法。 数学模型的图解描述:
图中D(x)是已知的离散序列,E(x)= D(x)+ a,拟合直线为y = k·x + b,找出适当的k和b使得直线y(x)完全穿过红色区域。 解题思路: (1)y(x)是未知的,先取个k和b的估值,如图中示意,可取k=1,b=0做为初始估值。 (2)找b的值:平移直线(改变b值),直到直线全部大等于D(x),设b值为b1时刚好超过所有的点,其中临界超过的点是D(x1)。继续平移,找到直线刚好全部小于E(x)时b的取值,记为b2。 如果b2>b1,显然有解,若k值保持不变,b取值(b1+b2)/ 2,那么b允许的误差为h = (b2-b1)/2,查找过程结束。如果b2<=b1则继续以下步聚。 (3)找k的值:以点D(x1)为固定点旋转直线,找出直线不超过E(x)时k的取值范围(k1,k2)。如果k2<=k1则无解,查找过程结束。否则,k取(k1+k2)/ 2。 (4)从第2步开始重复以上过程,直到成功为止。重复的过程中,k的取值是在原有基础上进一步缩小范围的。比如,第一次得到k的范围是1到2之间,第二次为1.5到3之间,那么k的取值不是取前者也不是取后者,而是取二者的交集(1.5,2),否则以上过程中k的取值无法收敛到有效范围之内,造成死循环而找不到解。其实,以D(x)中的任意一点为固定点,都可以得到k的上下界值k1和k2,对于一条能够通过红区的直线,必然能够满足所有k1和k2的约束。 以上得取了b允许的误差值h,如果b不变,k允许的误差为b/N,式中N为D(x)序列的总个数。 算法实现: 设f(x) = D(x) - y(x),设K(n,m)表示点E(n)到点D(m)连线的斜率。 那么f(x)表示y(x)距D(x)的纵向距离,f(x)+a表示y(x)距E(x)纵向距离。 (1)先取个k和b的初始估值。置k可能的取值范围为(k1,k2),这个范围要足够大。 (2)在x=0,1,2……上遍历f(x),求得f(x)的最大值f1和最小值f2及相应的x值x1、x2。那么f2+a就是f(x)+ a的最小值,也就是说f2+a是y(x)到E(x)的最小纵向距离。 (3)如果f1<f2+a则有解,b = b + (f2+a+f1)/2,h = (f2+a-f1)/2,并输出结果,程序结束。 (4)在x>x1上遍历K(x,x1),取得最小值k1(该最小必须须比原来的k1还要小,否则不算) 在x<x1上遍历K(x,x1),取得最大值k2(该最大必值须比原来的k2还要大,否则不算) 如果k1>=k2则无解,输出无解报告,程序结束。否则取k = (k1+k2)/2。 (5)从第2步开始重复计算,直到有解。注意, k1和k2是全过程中的最值,而不是某一次遍历过程中的最值。通常1到6次就能得到结果,如果重复计算10次仍无解,程序也应结束。 优化算法: 有时我们不走运,程序可以得到满足条件的直线,但h的值非常小。比如得到h = 0.000002,设N = 10000,那么k允许的误差为0.0000000002,也就是说k必须取10位有效小数才可保证结果的正确性。所以有必要提高h的值。以下描述本笔者提高h值的方法。 计算前,适当减小a,使得上图的红色区域变小,然后出k、b、h,如果k、b有解,那么相应的y(x)定能通过原来较大的红色区域,这样b的取值范围就变得宽裕了,h自然就比较大了。设a的原值记为A,那么只需将上述算法第3步改为:“如果f1<f2+a则有解,b = b + (f2+A+f1)/2,h = (f2+A-f1)/ 2,并输出结果,程序结束”,等价于“如果f1<f2+a则有解,h = (f2+A-f1)/2,b = b+f1+h,并输出结果,程序结束” 当然,a的值也不能减小过多。因为某些序列对拟合直线要求非常苛刻,理论上可找到的h值本身就非常小,这是a减小过多可能造成无解。寿星万年历的辅助程序中,减小量取值0.0002。 范例程序: 拟合之前先设定参数,以便生成序列。 |